Dos pares
ordenados son iguales, si y solo si son iguales sus respectivas componentes. Es
decir que (a,b) = (c=d) si y solo si a=c y b=d.
Ejemplo 1:
Determinar
el valor de las incógnitas x,y de la siguiente igualdad.
Primer paso,
igualar las abscisas y las oordenadas.
Recordar
siempre que un par ordenado está dado por dos componentes, (x,y) entonces,
igualamos las “x” y las “y”
, llamaremos a esta, primera ecuación. Y despejamos cualquiera de las dos
variables
que en este caso se encuentran.
Para resolver ecuaciones con dos variables, existen varios métodos, como
lo son, el método por sustitución, reducción, igualación entre otros. En este
caso, usaremos el método por sustitución.
, despejamos a la “x” teniendo en cuenta que el término de 3y estaba
negativo, y
cuando lo pasamos al otro lado del signo igual se convierte en
positivo. (Se dice, estaba restando y pasa a sumar)
Hasta ahora la variable “x” no está totalmente despejada puesto que debe
tener como coeficiente 1, entonces, el 2 que la acompaña está multiplicando y
pasa al otro lado del signo igual, a dividir.
, como no conocemos el valor de “y”, hacemos la igualación de las
oordenadas de los
pares ordenados.
Sustituimos en
la ecuación 1, el valor de “y” encontrado.
Hacemos la comprobación para verificar los resultados.
Tomamos la ecuación 1
En efecto, 7=7,
por tanto los resultados están correctos.
Para una mayor
comprensión, les dejo el video:




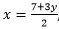


buen día inga. excelente tema el citado en este blog
ResponderBorrarEstimada compañera me parece interesante su blog, ya que hace su presentación de forma práctica y sencilla. Saludos!!!!!!!!
ResponderBorrarSi (3 + 7, 12) = (22, 2 − 6), encuentra el valor de la suma de x + y
ResponderBorrarmuy interesante la igualda de pares ordenados
ResponderBorrarHallar el valor de x,y que verifiquen la igualdad
ResponderBorrar(x-1),(y+1)=(2,3)
(x-2y),(3x-y)=(3,2)
ResponderBorrar